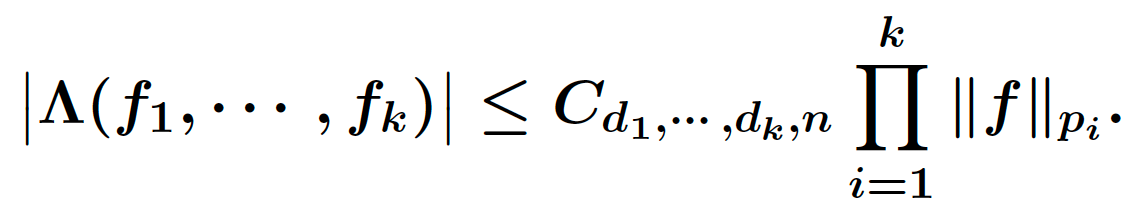In this talk, we investigate some necessary and sufficient conditions which ensure the validity of the k-Fold Beta integral formula. That is, the k-Fold Beta integral equation is as follows
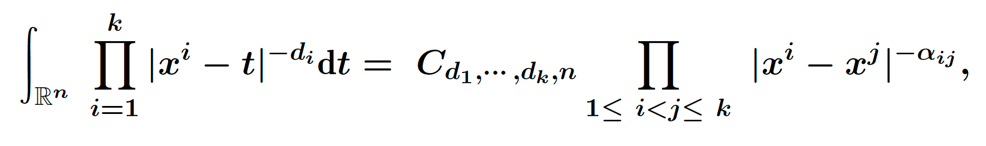
where $x^{i}\in \mathbb{R}^n$ $d_i$ is nonzero real number, with $i=1,\cdots,k$.
Actually, we completely answer the question raised by Grafakos. For some cases, we will prove that the constant number $C_{d_1,\cdots,d_k,n}$ is just the sharp bound of the following generalized Hardy-Littlewood -Sobolev inequality: